Producer-Consumer problem, Let's understand what is the problem? , Producer Code , Let's understand above Producer and Consumer code

 

Producer-Consumer problem

The Producer-Consumer problem is a classical multi-process synchronization problem, that is we are trying to achieve synchronization between more than one process.

There is one Producer in the producer-consumer problem, Producer is producing some items, whereas there is one Consumer that is consuming the items produced by the Producer. The same memory buffer is shared by both producers and consumers which is of fixed-size.

The task of the Producer is to produce the item, put it into the memory buffer, and again start producing items. Whereas the task of the Consumer is to consume the item from the memory buffer.

Let's understand what is the problem?

Below are a few points that considered as the problems occur in Producer-Consumer:

• The producer should produce data only when the buffer is not full. In case it is found that the buffer is full, the producer is not allowed to store any data into the memory buffer.
• Data can only be consumed by the consumer if and only if the memory buffer is not empty. In case it is found that the buffer is empty, the consumer is not allowed to use any data from the memory buffer.
• Accessing memory buffer should not be allowed to producer and consumer at the same time.

Let's see the code for the above problem:

Producer Code

Producer Code

Let's understand above Producer and Consumer code:

Before Starting an explanation of code, first, understand the few terms used in the above code:

1. "in" used in a producer code represent the next empty buffer
2. "out" used in consumer code represent first filled buffer
3. count keeps the count number of elements in the buffer
4. count is further divided into 3 lines code represented in the block in both the producer and consumer code.

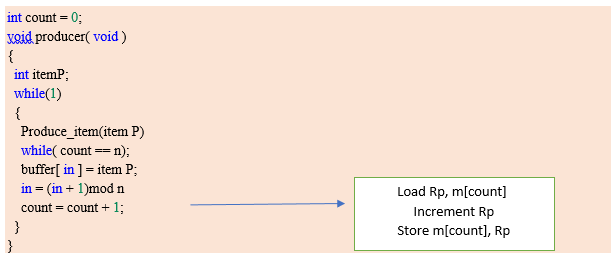
If we talk about Producer code first:

--Rp is a register which keeps the value of m[count]

--Rp is incremented (As element has been added to buffer)

--an Incremented value of Rp is stored back to m[count]

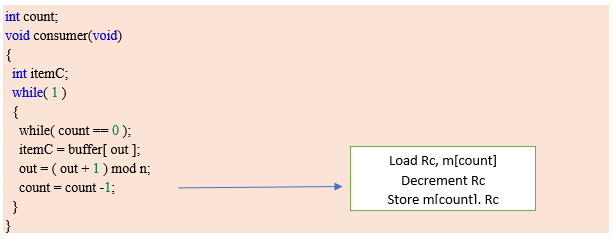
Similarly, if we talk about Consumer code next:

--Rc is a register which keeps the value of m[count]

--Rc is decremented (As element has been removed out of buffer)

--the decremented value of Rc is stored back to m[count].

BUFFER

As we can see from Fig: Buffer has total 8 spaces out of which the first 5 are filled, in = 5(pointing next empty position) and out = 0(pointing first filled position).

Let's start with the producer who wanted to produce an element " F ", according to code it will enter into the producer() function, while(1) will always be true, itemP = F will be tried to insert into the buffer, before that while(count == n); will evaluate to be False.

Buffer[in] = itemP → Buffer[5] = F. ( F is inserted now)

in = (in + 1) mod n → (5 + 1)mod 8→ 6, therefore in = 6; (next empty buffer)

After insertion of F, Buffer looks like this

Where out = 0, but in = 6

Since count = count + 1; is divided into three parts:

Load Rp, m[count] → will copy count value which is 5 to register Rp.

Increment Rp → will increment Rp to 6.

Suppose just after Increment and before the execution of third line (store m[count], Rp) Context Switch occurs and code jumps to consumer code. . .

Consumer Code:

Now starting consumer who wanted to consume the first element " A ", according to code it will enter into the consumer() function, while(1) will always be true, while(count == 0); will evaluate to be False( since the count is still 5, which is not equal to 0.

Note: Semicolon after while loop will not let the code to go ahead if it turns out to be True( i.e. infinite loop/ no element in buffer)

itemC = Buffer[out]→ itemC = A ( since out is 0)

out = (out + 1) mod n → (0 + 1)mod 8→ 1, therefore out = 1( first filled position)

A is removed now

After removal of A, Buffer look like this

Where out = 1, and in = 6

Since count = count - 1; is divided into three parts:

Load Rc, m[count] → will copy count value which is 5 to register Rp.

Decrement Rc → will decrement Rc to 4.

store m[count], Rc → count = 4.

Now the current value of count is 4

Suppose after this Context Switch occurs back to the leftover part of producer code. . .

Since context switch at producer code was occurred after Increment and before the execution of the third line (store m[count], Rp)

So we resume from here since Rp holds 6 as incremented value

Hence store m[count], Rp → count = 6

Now the current value of count is 6, which is wrong as Buffer has only 5 elements, this condition is known as Race Condition and Problem is Producer-Consumer Problem.

The solution of Producer-Consumer Problem using Semaphore

The above problems of Producer and Consumer which occurred due to context switch and producing inconsistent result can be solved with the help of semaphores.

To solve the problem occurred above of race condition, we are going to use Binary Semaphore and Counting Semaphore

Binary Semaphore: In Binary Semaphore, only two processes can compete to enter into its CRITICAL SECTION at any point in time, apart from this the condition of mutual exclusion is also preserved.

Counting Semaphore: In counting semaphore, more than two processes can compete to enter into its CRITICAL SECTION at any point of time apart from this the condition of mutual exclusion is also preserved.

Semaphore: A semaphore is an integer variable in S, that apart from initialization is accessed by only two standard atomic operations - wait and signal, whose definitions are as follows:

1. 1. wait( S )  
2. {  
3. while( S <= 0) ;  
4. S--;  
5. }  

1. 2. signal( S )  
2. {  
3. S++;  
4. }  

From the above definitions of wait, it is clear that if the value of S <= 0 then it will enter into an infinite loop (because of the semicolon; after while loop). Whereas the job of the signal is to increment the value of S.

Let's see the code as a solution of producer and consumer problem using semaphore ( Both Binary and Counting Semaphore):

Producer Code- solution

1. void producer( void )  
2. {  
3.   wait ( empty );  
4.   wait(S);  
5.   Produce_item(item P)  
6.   buffer[ in ] = item P;  
7.   in = (in + 1)mod n  
8.   signal(S);  
9.   signal(full);  
10.     
11. }  

Consumer Code- solution

1. void consumer(void)  
2. {  
3.   wait ( empty );  
4.   wait(S);  
5.   itemC = buffer[ out ];  
6.   out = ( out + 1 ) mod n;  
7.   signal(S);  
8.   signal(empty);  
9. }  

Let's understand the above Solution of Producer and Consumer code:

Before Starting an explanation of code, first, understand the few terms used in the above code:

1. "in" used in a producer code represent the next empty buffer
2. "out" used in consumer code represent first filled buffer
3. "empty" is counting semaphore which keeps a score of no. of empty buffer
4. "full" is counting semaphore which scores of no. of full buffer
5. "S" is a binary semaphore BUFFER

If we see the current situation of Buffer

S = 1(init. Value of Binary semaphore

in = 5( next empty buffer)

out = 0(first filled buffer)

As we can see from Fig: Buffer has total 8 spaces out of which the first 5 are filled, in = 5(pointing next empty position) and out = 0(pointing first filled position).

Semaphores used in Producer Code:

6. wait(empty) will decrease the value of the counting semaphore variable empty by 1, that is when the producer produces some element then the value of the space gets automatically decreased by one in the buffer. In case the buffer is full, that is the value of the counting semaphore variable "empty" is 0, then wait(empty); will trap the process (as per definition of wait) and does not allow to go further.

7. wait(S) decreases the binary semaphore variable S to 0 so that no other process which is willing to enter into its critical section is allowed.

8. signal(s) increases the binary semaphore variable S to 1 so that other processes who are willing to enter into its critical section can now be allowed.

9. signal(full) increases the counting semaphore variable full by 1, as on adding the item into the buffer, one space is occupied in the buffer and the variable full must be updated.

Semaphores used in Producer Code:

10.0wait(full) will decrease the value of the counting semaphore variable full by 1, that is when the consumer consumes some element then the value of the full space gets automatically decreased by one in the buffer. In case the buffer is empty, that is the value of the counting semaphore variable full is 0, then wait(full); will trap the process(as per definition of wait) and does not allow to go further.

11. wait(S) decreases the binary semaphore variable S to 0 so that no other process which is willing to enter into its critical section is allowed.

12. signal(S) increases the binary semaphore variable S to 1 so that other processes who are willing to enter into its critical section can now be allowed.

13. signal(empty) increases the counting semaphore variable empty by 1, as on removing an item from the buffer, one space is vacant in the buffer and the variable empty must be updated accordingly.

Producer Code:

Let's start with producer() who wanted to produce an element " F ", according to code it will enter into the producer() function.

wait(empty); will decrease the value of empty by one, i.e. empty = 2

Suppose just after this context switch occurs and jumps to consumer code.

Consumer Code:

Now starting consumer who wanted to consume first element " A ", according to code it will enter into consumer() function,

wait(full); will decrease the value of full by one, i.e. full = 4

wait (S); will decrease the value of S to 0

itemC = Buffer[out]; → itemC = A ( since out is 0)

A is removed now

out = (out + 1) mod n → (0 + 1)mod 8 → 1, therefore out = 1( first filled position)

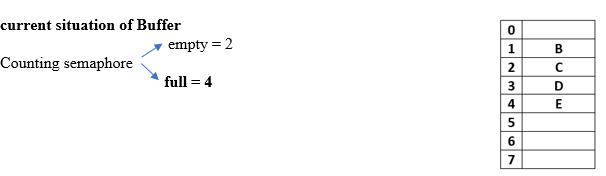
S = 0(Value of Binary semaphore)

in = 5( next empty buffer)

out = 1(first filled buffer)

Suppose just after this context, switch occurs back to producer code

Since the next instruction of producer() is wait(S);, this will trap the producer process, as the current value of S is 0, and wait(0); is an infinite loop: as per the definition of wait, hence producer cannot move further.

Therefore, we move back to the consumer process next instruction.

signal(S); will now increment the value of S to 1.

signal(empty); will increment empty by 1, i.e. empty = 3

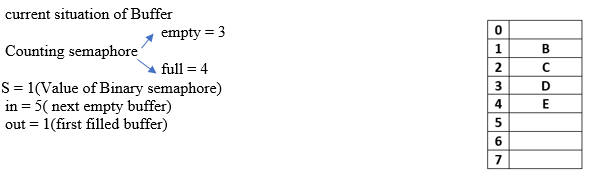
Now moving back to producer() code;

Since the next instruction of producer() is wait(S); will successfully execute, as S is now 1 and it will decrease the value of S by 1, i.e. S = 0

Buffer[in] = itemP; → Buffer[5] = F. ( F is inserted now)

in = (in + 1) mod n → (5 + 1)mod 8 → 6, therefore in = 6; (next empty buffer)

signal(S); will increment S by 1,

signal(full); will increment full by 1, i.e. full = 5

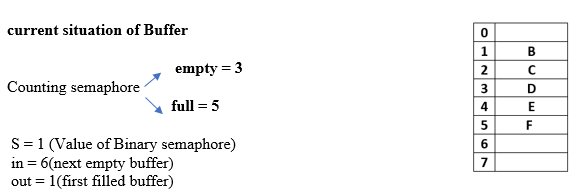
Now add current value of full and empty, i.e. full + empty = 5 + 3 = 8(which is absolutely fine) No inconsistent result is generated even after so many context switches. But in the previous condition of producer and consumer without semaphore, we see the inconsistent result in case of context switches.

This is the solution to the Producer consumer problem.